Los jugadores reciben puntos por cada par de fichas encontradas. El jugador con la mayor cantidad de puntos gana. Los puntos se calculan de la siguiente manera:
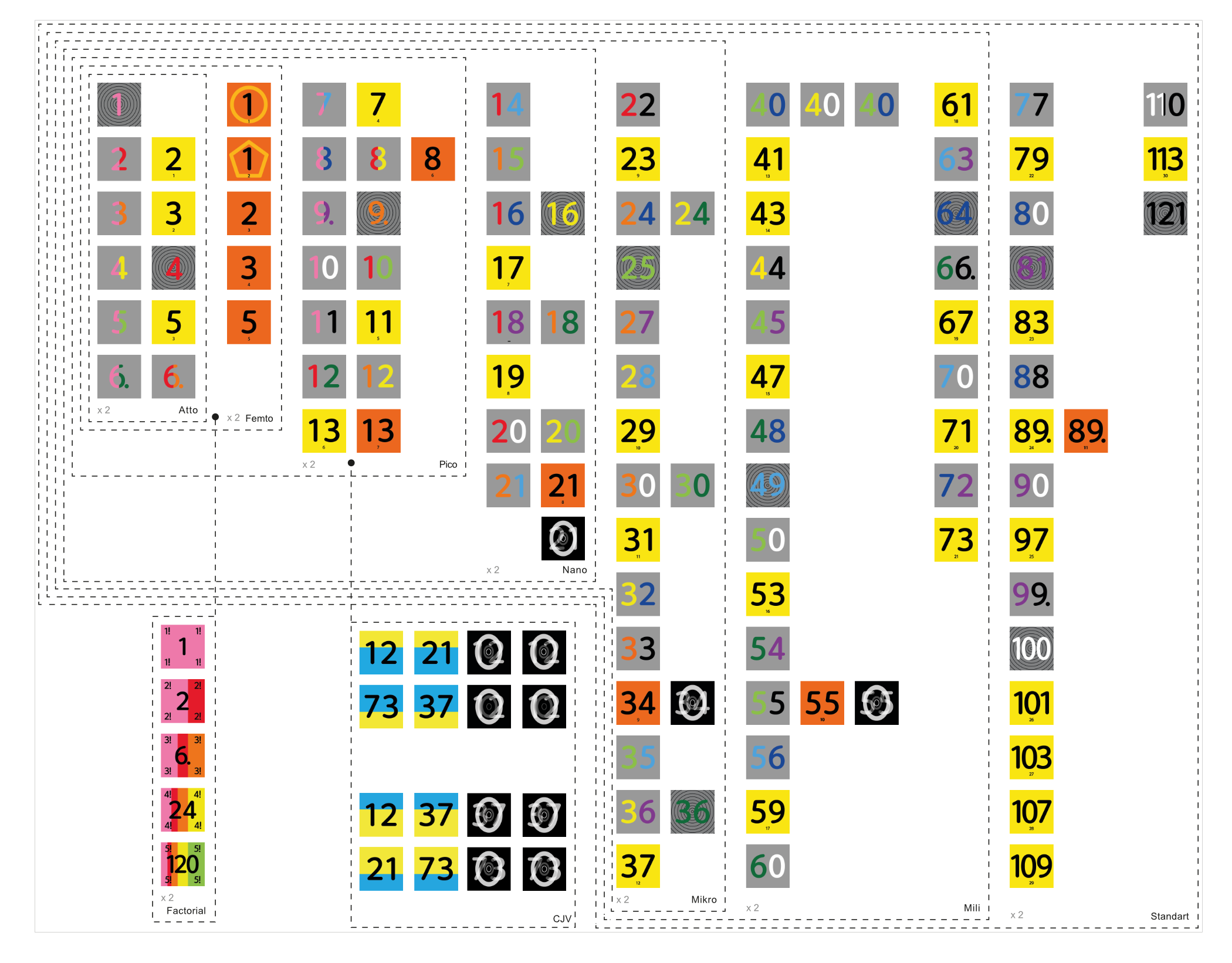
- $0$ puntos por cada par del grupo cero (fondo negro).
- $1$ punto por cada par del grupo de números primos (fondo amarillo).
- $2$ puntos por cada par del grupo de números de Fibonacci (fondo naranja).
- $2$ puntos por cada par del grupo de pequeños múltiplos (fondo de colores sobre fondo gris)
- $3$ puntos por cada par del grupo de potencias (fondo de colores sobre fondo circular)
- $4$ puntos por cada par del grupo de factoriales (fondo arcoíris)
- $5$ puntos por cada par del grupo CJV (fondo azul y amarillo)
Puntos por combinaciones de varias categorías
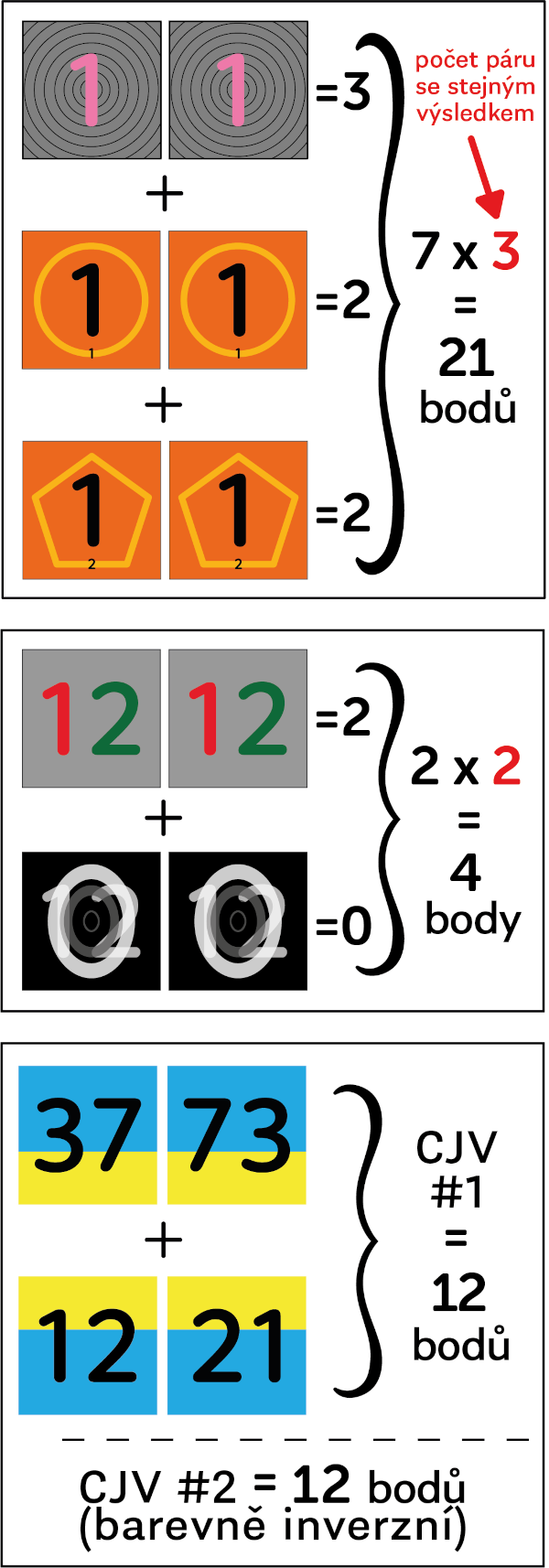
Si un jugador tiene varios pares con el mismo valor numérico, los puntos por estos pares se suman y se multiplican por el número de pares con ese valor numérico.
Ejemplo:
2121 y también
2121El jugador ganó 2 puntos por el par de números Fibonacci y 2 puntos por el par de números pequeños de multiplicación. Eso es un total de 4 puntos. Como estos pares tienen el mismo valor numérico en el lado de color (ambos tienen el número $21$ en el lado de color), los puntos obtenidos se multiplican por dos, para un total de 8 puntos.
Ejemplo:
1616 y también
1616El jugador ganó 3 puntos por potencias y 2 puntos por pequeños números de multiplicación. Como estas cartas tienen el mismo valor numérico, la suma de puntos obtenidos se multiplica por 2, es decir, $(3+2) \cdot 2 = 10$. En total, el jugador obtiene 10 puntos.
Esta regla no se aplica a los pares de la categoría de factoriales y CJV.
Las tarjetas de la categoría cero no agregan puntos por sí mismas, sino que multiplican los puntos obtenidos por otros pares que tienen el mismo número en el lado de color que el número en el fondo de la tarjeta cero.
Ejemplo:
1212 y al mismo tiempo
1212El jugador obtuvo 2 puntos por el par de pequeñas multiplicaciones y 0 puntos por el par de ceros. Sin embargo, estos ceros tienen el número 12 en el fondo, lo que significa que multiplican por 2 los puntos por cada otro par con el valor numérico 12. Por lo tanto, el jugador obtiene 4 puntos.
Si el jugador obtuviera, por ejemplo, un par de ceros con el número transparente 11 en el fondo, multiplicaría este par con otras fichas con el número 11.
Un jugador que obtiene dos pares en la variante dada (llamada Sheldon) con CJV obtiene 12 puntos y también una jugada adicional en cualquier momento durante el juego.