Players receive points for each pair of jettons found. The player with the highest number of points wins. Points are counted as follows:
- $0$ points for each pair in the Zero group (black background)
- $1$ point for each pair in the Prime number group (yellow background)
- $2$ points for each pair in the Fibonacci group (orange background)
- $2$ points for each pair in the Multiplication table group (bicolor number on a gray background)
- $3$ points for each pair in the Power group (unicolor number on a circular background)
- $4$ points for each pair in the Factorial group (rainbow background)
- $5$ points for each pair in the CJV group (yellow-blue background)
Points for combinations from multiple groups
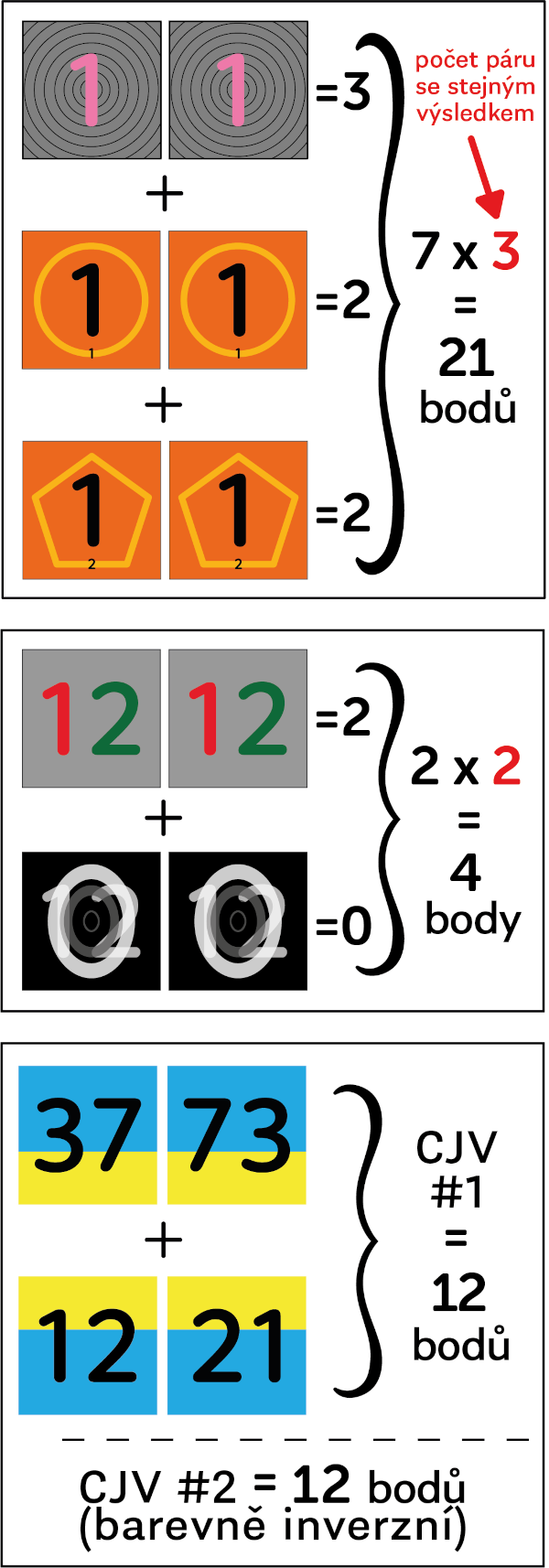
If a player has more than one pair with the same numerical value, the points for these pairs are added up and multiplied by the number of pairs with this numerical value.
Example:
2121 and
2121Thus, the player receives 2 points for a pair in Fibonacci number group and 2 points for a pair in Multiplication table group. That makes 4 points. Since these pairs have the same numerical value on the color side (both have number $21$ on the color side), the points obtained are multiplied by two which equals 8 points in total.
Example:
1616 and
1616Thus, the player gets 3 points for a pair in Power group and 2 points for a pair in Multiplications table group. Since these cards have the same numerical value, the sum of the obtained points is multiplied twice, ie $(3+2) \cdot 2 = 10$. In total, the player gets 10 points.
This rule does not apply to factorials and CJV pairs.
Zero group pairs do not add points per se,but multiply the number of points for certain other pairs that have the same number on the color side as is the translucent number in the background.
Example:
2121 and
2121Thus, the player receives 2 points for a pair in Multiplication table group and 0 points for a pair of zeros. However, these zeros have translucent number $21$ in the background, which means that the points multiply twice for every other pair with the numerical value $21$, ie $(2+0) \cdot 2=4 $ points.
For example, if a player got a pair of zeros with translucent number $11$ in the background, that pair would multiply another pair with number $11$.
A player who gets two pairs in a given variant (so-called Sheldon) with CJV gets 12 points and one extra move at any time during the game.